ما هو تعريف السرعة

تم التدقيق بواسطة: فريق أراجيك
السرعة (Speed) هي مقدارٌ فيزيائيٌّ يعبّر عن المسافة التي يقطعها جسم ما أثناء حركته خلال واحدة الزمن، وتمثّل القيمة العدديّة لمتجّه السرعة أو كما يُسمّى أيضًا شعاع السّرعة (Velocity)، أي أنّ السّرعة لا تعبّر عن اتجاهٍ؛ وإنّما تُعنى فقط بالقيمة العدديّة لشعاع السرعة، وكلّما زادت قيمة السرعة فهذا يعني أنّ الجسم يتحرك بشكلٍ أسرع، وفي حال كان الجسم ساكنًا، فهذا يعني أنّ سرعته تساوي الصفر..
معادلة حساب السرعة
القانون الأشهر والأكثر شيوعًا لقياس سرعة جسم يتحرّك بحركةٍ مستقيمةٍ:
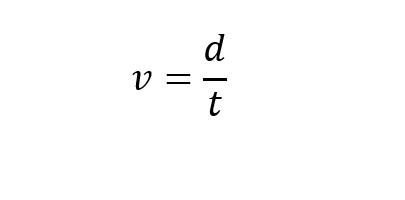
حيث أنّ:
- v: السرعة.
- d: المسافة المقطوعة.
- t: الزمن.
تُسمّى المقادير الثلاثة التي تشمل السرعة والمسافة والزمن بالمتغيّرات، حيث يؤثّر كل مقدارٍ منها على الآخر، كما أنّ هذه المقادير تختلف من تجربةٍ إلى أخرى، ويجدر الانتباه إلى أنّ سرعة الجسم تتناسب بشكلٍ طرديٍّ مع المسافة وبشكلٍ عكسيٍّ مع الزمن، أي كلمّا زادت المسافة زادت السرعة والعكس صحيح، وكلمّا زاد الزمن نقصت سرعة الحركة وأيضًا العكس صحيح..
سرعة الجسم المتوسّطة
يعبّر مصطلح السرعة المتوسطة عن متوسط المسافة المقطوعة خلال زمنٍ معيّنٍ، فعلى سبيل المثال ليكن لدينا سيارة انطلقت من النقطة (1) إلى النقطة (2)، خلال الرحلة تكون سرعة السيارة متغيّرةً بشكلٍ مستمرٍ أيّ أنّها لا تسير وفق سرعة ثابتة، فتارة تُسرع وتارة تُبطء وقد تتوقّف لفتراتٍ قصيرةٍ بسبب وجود إشارات مرورٍ، لذلك عند وصف سرعة هذه السيارة باستخدام مفهوم السرعة المتوسّطة، فنحن نقيس المسافة الكليّة التي قطعتها السيارة ونقيس الزمن الكليّ للرحلة، ونحسب سرعة تعبّر عن القيمة المتوسّطة التي تتخللّ سرعات كبيرة وسرعات صغيرة وتوقفّات، وفي هذه الحالة نستخدم قانون السرعة والذي قد نجده بشكلٍ مختلفٍ قليلًا عن الشكل السابق:
يشير الرمز Δ إلى التغيّر، كما يشير الرمز v إلى سرعة الجسم المتوسّطة.
مثال عمليّ: انطلقت سيارة من نقطة (1) إلى نقطة (2) تبعد عنها مسافة 200 كم، استغرقت الرحلة 4 ساعاتٍ، لحساب السرعة:
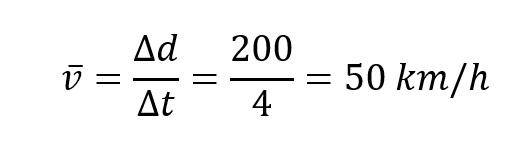
سرعة الجسم الآنيّة (اللحظيّة)
تعبّر عن سرعة الجسم في لحظةٍ معيّنةٍ دون غيرها، ويمكن أن نراها في عدّاد السرعة الخاص بالسيارة، إذ أنّه يتغيّر بشكلٍ دائمٍ تبعًا لسرعة السيّارة.
من الناحيّة الرياضيّة، تعبّر السرعة الآنيّة عن سرعة جسمٍ خلال فاصلٍ زمنيٍّ صغير جدًا، ويكون أقرب ما يمكن إلى الصفر، يُعبّر عن ذلك رياضيًّا باستخدام مفهوم النهايات، أي أنّ تغير الزمن يسعى إلى الصفر وبالتالي يكون قانون السرعة بالشكل التالي:
حيث أنّ d تعني تغيّرًا ضئيلًا جدًا، وهذا ما يُسمّى بالاشتقاق الرياضيّ، إذ أنّ السرعة الآنيّة هي مشتق المسافة بالنسبة للزمن، ويعبّر عنها رياضيًّا بالشكل التالي: .
واحدات القياس للسرعة
توجد العديد من الواحدات لقياس السرعة وذلك يعتمد على نظام الواحدات المتّبع في الدولة، وفيما يلي واحدة السرعة في أكثر أنظمة القياس انتشارًا:
- جملة الواحدات الدوليّة (SI): تقاس بواحدة متر/ثانية (m/s) أو بشكل آخر متر×ثانية-1 (m.s-1).
- جملة الواحدات السغثية (CGS): تقاس بواحدة سم/ثانية (cm/s) أو بشكل آخر سم×ثانية-1 (cm.s-1).
كما تقاس بواحداتٍ أخرى تخدم غرض القياس، فعلى سبيل المثال تقاس سرعة السيارات بواحدة (كم/ساعة) في النظام المتري، بينما تقاس بواحدة (ميل/ساعة) في نظام القياس الأمريكيّ..
الفرق بين السرعة وشعاع السرعة
الفرق الجوهري بين كلٍ من السرعة (Speed) وشعاع السرعة (Velocity) هو أنّ الأولى تعبّر عن عددٍ فقط، وهو قيمة سرعة الجسم الناتج عن تقسيم المسافة التي قطعها الجسم خلال زمنٍ ما، بينما الثاني يعبّر عن اتجاه سرعة الحركة مرفوقًا بالعدد الذي يمثّل قيمة سرعة الجسم، ولتوضيح الفكرة بشكلٍ أفضل سنشرح مفهومين جديدين وهما:
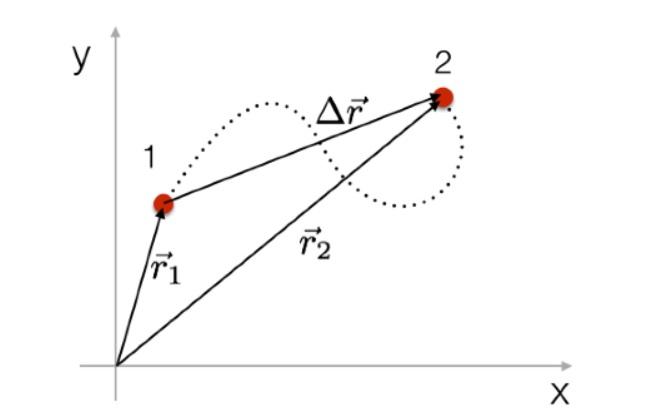
- شعاع الإزاحة: ليكن لدينا جسم يتحرّك من النقطة 1 إلى النقطة 2، يعبّر شعاع الإزاحة عن الشعاع المتجّه من النقطة الأولى إلى النقطة الثانية، ويحسب من خلال العلاقة التالية:
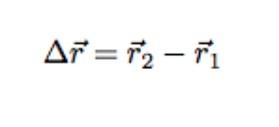
- لا يتعلّق شعاع الإزاحة بمبدأ الإحداثيات، إنّما يتم تعريفه فقط بمعرفة النقطتين اللتين ينتقل بينهما الجسم، وحساب شعاع الإزاحة لا يتطلب منّا معرفة مكان إنطلاق الجسم بالحركة أو مكان توقفّه بالنسبة للمبدأ.
- شعاع الموضع: شعاع الموضع للنقطة الأولى هو الشعاع المتّجه من المبدأ إلى هذه النقطة، وبالتالي إذا تغيّر موقع مبدأ الإحداثيات ستتغير قيمة شعاع الموضع.
بذلك يمكن القول أنّ السرعة (Speed) هي القيمة العددية لشعاع الإزاحة مقسومة على زمن الحركة، أي أنّه يكفي معرفة قيمة المسافة التي انتقلها الجسم وزمن الانتقال بغض النظر عن المسار الذي اتّبعه الجسم أثناء الحركة، بينما لحساب شعاع السّرعة (Velocity) فيجب عليك معرفة شعاع الموضع لنقطة بداية الحركة، وشعاع الموضع لنقطة نهاية الحركة أي أنّه من المهم معرفة المسار والاتجاه الذي يسلكه الجسم أثناء حركته. .
 ذكاء اصطناعي
ذكاء اصطناعي أجهزة ذكية
أجهزة ذكية ريادة
ريادة أعظم الكتب
أعظم الكتب هواتف
هواتف توب التوب
توب التوب منصات
منصات عملات رقمية
عملات رقمية